 삼각함수 미분 쉽게외우기!!
삼각함수 미분 쉽게외우기!!
그림으로 보면 뭐야(?) 하겠지만 이해만하면 이보다 쉽게 외울 순 없다. 1. 그림에서 O는 출발지 D는 도착지를 나타낸다. 2. sinㅡcos가 있는 첫번째 줄은 서로교환하며 tanㅡ1ㅡcot가 있는 두번째 줄에서 아래로 내려갈때는 도착지의 제곱을 해주면되고 sec와 csc가 있는 세번째 줄에서 위로 올라갈때는 출발지와 도착지의 곱이라고 생각하면 된다. (-) 기호를 잘 살펴봐야하는데 c로 시작하는 곳(cos, cot, csc)에서 시작하면 (-) 기호가 붙는다. 3. 나열해보면 다음과 같다. (sin)` = cos (cos)` = -sin (tan)` = sec² (sec)` = sectan (cot)` = -csc² (csc)` = -csccot
study/mathematics
2011. 5. 11. 03:10
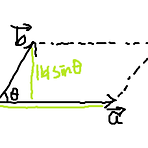 11.4> 벡터곱
11.4> 벡터곱
1. 두 벡터 a와 b의 곱 a X b의 결과는 내적과는 달리 벡터이다. 벡터곱 또는 외적이라고 부르기도하며, 이것은 3차원 벡터일 경우에만 정의된다. 2. 벡터 (a X b) 는 a와 b 모두에 수직한다. 수직의 방향은 '오른손 법칙'에 따라 주어지며 시작 벡터는 a, 끝 벡터는 b이다. 두개의 수직하는 벡터를 구할 땐 [1] (a X b) 와, [2] -(a X b) 를 구하면 된다. 3. 벡터곱의 크기인 la X bl 는 lallblsinθ 와 같으며 이는 벡터 a와 b에 의해 결정되는 평행 사변형의 넓이(밑변x높이)와 같다.
study/mathematics
2011. 4. 3. 22:16

